Másodfokú függvény

Általában a független változót x -szel, a függő változót y-nal, magát a függvényt pedig f-fel jelöljük. A független változót argumentumnak is nevezzük. Az argumentum (x) összes értékeinek halmazát a függvény értelmezési tartományának nevezzük és D ( f )-fel vagy D (y)-nal jelöljük

A függvény egyértelmű hozzárendelés, tehát az x  argumentum minden értékéhez csak egy függő y  érték tartozik. A függő változó értékét a függvény helyettesítési értékének nevezzük és f(x) –szel jelöljük. A függő változó (y)  összes értékének halmaza a függvény értékkészlete. Jelölése E ( f ) vagy E (y ).

Meghatározás. Az argumentum azon értékét, amelynél a függvényérték nulla, a függvény zérushelyének nevezzük.

Meghatározás. Azt az intervallumát, amelyen a függvényérték előjele nem változik, állandó előjelű intervallumnak nevezzük.

Meghatározás.  Az f függvény növekvő egy adott intervallumon, ha bármely, az adott intervallumhoz tartozó x1 és x2 esetében x1 > x2 argumentum értékekre igaz az f(x1) > f(x2) egyenlőtlenség.

Meghatározás. Az f függvény csökkenő egy adott intervallumon, ha bármely, az adott intervallumhoz tartozó x1 és x2 esetében x1 > x2 argumentum értékekre igaz az f(x1) < f(x2) egyenlőtlenség.

Gyakran használjuk az alábbi meghatározást is.

Meghatározás. A függvény növekvő egy adott intervallumon, ha bármely, az adott intervallumhoz tartozó argumentum értékekre teljesül, hogy nagyobb argumentumhoz nagyobb függvényérték tartozik.

Meghatározás. A függvény csökkenő egy adott intervallum on, ha bármely, az adott intervallumhoz tartozó argumentum értékekre teljesül, hogy nagyobb argumentumnak kisebb függvényérték felel meg.

Az y = k f (x) függvény grafikonját, ahol k > 0 megkapjuk, ha az y = f (x) függvény minden pontjának az ordinátáját k - szorosára növeljük. (A k - szoros nyújtással az y tengely mentén (az x tengelytől), ha k > 1, és 1k  - szoros zsugorítással az y tengely menten (az x tengelyhez), ha 0 < k < 1.)

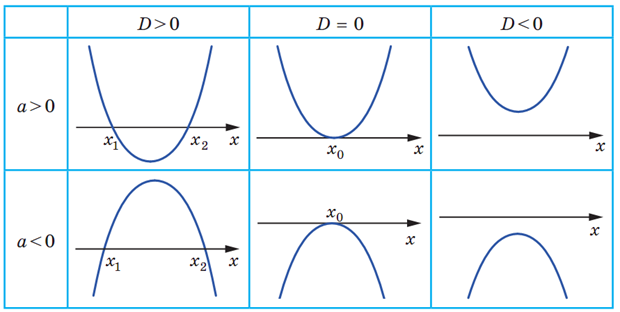
Az y = ax2 függvény grafikonja parabola. Ha a> 0, akkor a parabola szárai felfelé mutatnak, ha a <0, akkor pedig lefelé.

Az y = f (x) + b megkapható az y =f(x) függvény grafikonjából párhuzamos eltolással az y tengely mentén b egységgel felfelé, ha b > 0 és lefelé, ha b < 0.

Az y = f (x + a) megkapható az y = f (x) függvény grafikonjából párhuzamos eltolással az x tengely mentén a egységgel balra, ha a > 0 és jobbra, ha a < 0.

Az у = k (х + a)2+ b, k≠0  függvény grafikonja parabola, mégpedig olyan, mint az у = kх2 függvényé, a csúcsa pedig a (-a; b) koordinátájú pont.

Az y = ax2 + bx + c képlettel megadott függvényt, ahol a, b és c valós szám, x az argumentum, a ≠  0, másodfokú függvénynek nevezzük.

A másodfokú függvényt az alábbi algoritmussal lehet ábrázolni:

1. Az x0=-b2a  képlettel meghatározzuk a parabola csúcsának abszcisszáját;
2. Az y0=4ac-b24a=-D4a   képlettel meghatározzuk a parabola csúcsának ordinátáját, ahol D az ax2 + bx + c másodfokú polinom gyöke, majd koordinátarendszerben feltüntetjük a parabola csúcsát;
3. Meghatározzuk a parabola szárainak irányát;
4. Meghatározunk még néhány olyan pontot, melyek illeszkednek a grafikonra, például a parabola és az abszcisszatengely metszéspontjait (ha függvénynek vannak zérushelyei), vagy a parabola és az ordinátatengely metszéspontjának koordinátáit;
5. Feltüntetjük ezeket a pontokat a koordinátarendszeren;
6. Folytonos vonallal összekötjük a feltüntetett pontokat.

Az y = ax2 + bx + c parabola elhelyezkedése a koordinátarendszerben.